О среднем арифметическом значении мы знаем еще со школы. Но как его использовать, если больше не нужно решать задачи по математике? Разберемся с этим и объясним, почему среднее арифметическое — не единственный способ найти тенденции в ряду значений.
Что такое среднее арифметическое
Среднее арифметическое — это математический способ найти «среднее» значение группы чисел. Чтобы его вычислить, нужно сложить все числа вместе и затем разделить полученную сумму на количество этих чисел.
Например, у нас есть числа 2, 4 и 6. Складываем их: 2 + 4 + 6 = 12. Делим сумму на количество чисел: 12 / 3 = 4
Среднее арифметическое этих чисел — 4. Это значит, что, если бы все три числа были одинаковыми, они бы равнялись 4.
Формула для среднего арифметического
Формула для вычисления среднего арифметического выглядит так:
Где:
- х — это искомое среднее арифметическое;
- числитель — все значения, которые у нас есть;
- n — количество всех чисел в ряду.
В чём проблема среднего арифметического
Среднее арифметическое полезно для разных вычислений, но у него есть несколько ограничений.
Влияние выбросов (экстремальных значений)
Если в наборе чисел есть очень большие или очень маленькие значения (выбросы), они могут сильно исказить среднее арифметическое. Например, в наборе {1, 2, 3, 1000} среднее арифметическое будет 251,5. Но оно не отражает реальной картины: большинство чисел в выборке гораздо меньше.
Подходит не для всех типов данных
Среднее арифметическое имеет смысл только для числовых данных, которые можно складывать и делить. Для категориальных данных или рангов не имеет смысла его использовать.
Не отражает распределение
Среднее арифметическое не показывает, как распределены данные. Два набора с одинаковым средним арифметическим могут иметь совершенно разное распределение. Например, набор {1, 1, 1, 1, 5} и набор {1, 2, 3, 4, 5} имеют одно и то же среднее значение, но очень разные распределения.
Не всегда интуитивно понятно
В некоторых ситуациях среднее арифметическое может не давать интуитивно понятного представления о данных. Например, средняя температура на улице в течение всего дня может быть +10 °C, но это не говорит о том, что всё это время на улице было комфортно.
Из-за этих проблем в некоторых случаях используют другие значения — медиану или моду, которые дают более точное представление о данных.
Среднее значение — важный показатель в мире аналитики данных. Если хотите узнать об этой сфере подробнее, записывайтесь на консультацию и узнайте больше о курсе Skypro «Аналитик данных».
Что такое медиана
Медиана — это значение, которое находится в середине упорядоченного набора чисел. Она делит этот набор на две равные части: половина чисел меньше медианы, а другая половина — больше.
Например, у нас есть числа 3, 1, 4. Сначала их нужно упорядочить по возрастанию: 1, 3, 4. Медиана здесь — 3, потому что это число находится посередине.
Если количество чисел четное, медиана будет средним арифметическим двух средних чисел. Например, для чисел 1, 2, 3, 4 медиана будет (2 + 3) / 2 = 2,5.
Что такое мода
Мода — это значение, которое встречается чаще всего в наборе данных, самый распространенный элемент в числовом ряду.
Например, если у нас есть набор чисел: 1, 2, 2, 3, 4, 4, 4, 5, то мода будет 4 — это число встречается чаще всего (три раза).
Мода не зависит от экстремальных значений, поэтому ее часто используют при анализе данных с выбросами. К тому же мода подходит для работы с категориальными данными — когда нужно найти самый часто повторяющийся объект.
Формулы для моды как таковой нет, потому что ее считают вручную: смотрят, насколько часто повторяется значение в ряду.
Как найти моду:
- Записать все значения из набора данных.
- Подсчитать, сколько раз встречается каждое значение.
- Найти значение, которое встречается чаще других. Это и будет мода.
В каких сферах нужны эти значения
Среднее арифметическое используют для анализа данных в различных сферах.
🟡 В экономике и финансах:
- рассчитать среднюю заработную плату;
- проанализировать средние доходы и расходы;
- оценить цены на товары и услуги.
🟡 В образовании:
- вычислить средний балл учеников;
- проанализировать средний балл по экзаменам или тестам.
🟡 В науке:
- вычислить значения в экспериментах;
- обобщить данные в исследованиях (например, среднюю температуру, рост, вес).
🟡 В маркетинге и бизнесе:
- оценить стоимость товаров в ассортименте;
- проанализировать прибыль или убытки.
🟡 В медицине — вычислить средние показатели здоровья (например, артериальное давление, уровень сахара в крови).
Медиана бывает полезнее в отдельных областях.
🟢 В социальных науках — для анализа распределения доходов (медианный доход часто более информативен, чем средний) или оценки медианного возраста населения.
🟢 В экономике важны такие показатели: медианная цена недвижимости и медианный доход или уровень благосостояния, который часто нужен, чтобы оценить реальную картину в обществе.
🟢 В образовании медиана пригодится при анализе медианного балла, чтобы лучше понять успеваемость группы, особенно если есть выбросы — экстремальные значения. В контексте образования это либо круглые отличники, либо двоечники.
🟢 В медицине оценивают медианный процент выживаемости пациента после определенных процедур или операций.
🟢 В спорте анализируют медианой время или результат в соревнованиях. Или медианное время завершения марафона.
Среднее арифметическое хорошо отражает данные, когда значения распределены достаточно равномерно и нет экстремальных выбросов. Медиана работает лучше, когда в данных есть выбросы: она менее чувствительна к экстремальным значениям и лучше отражает типичное значение.
Кроме подсчета медианы и средних значений во всех этих областях нужны аналитики данных. Эти специалисты не просто работают с цифрами и табличками. Их задача — помочь бизнесу принять лучшее решение на основе данных. Получить эту профессию вы можете в онлайн-университете Skypro.
Какое значение выбрать
При выборе между медианой, средним арифметическим и модой учитывайте, как их интерпретируют и применяют в вашей сфере.
➕ Преимущество медианы: это устойчивая мера, которая отражает центральную тенденцию в ряде данных и нечувствительна к экстремальным значениям.
➕ Преимущество среднего арифметического: интуитивно понятная мера, подходит для симметричных распределений — без выбросов.
➕ Преимущество моды: полезна для описания типичных значений в данных с ярко выраженными пиками. Ее используют в анализе нечисловых значений: цвета, категории товаров и т. д.
Как вычислять значения в SQL
SQL (Structured Query Language) — это стандартизированный язык программирования для управления базами данных. В SQL есть команды для разных операций с данными. В том числе — для вычисления средних значений.
Рассмотрим, как с помощью SQL работать со средним арифметическим, медианой и модой.
Среднее арифметическое
В SQL вы можете использовать функцию AVG() для вычисления среднего арифметического значения в столбце.
SELECT AVG(column_name) AS average_value
FROM table_name;
Column_name — имя столбца, для которого вы хотите найти среднее значение.
Table_name — имя таблицы с этим столбцом.
Например, если у вас есть таблица grades с колонкой score и вы хотите найти средний балл, запрос будет выглядеть так:
SELECT AVG(score) AS average_score
FROM grades;
Мода
В SQL нет встроенной функции для вычисления моды, но вы можете написать собственный запрос или подзапрос. Например, сначала найти наиболее часто встречающееся значение в столбце, а затем отфильтровать только те значения, которые встречаются столько же раз, сколько и мода.
Пример запроса, который вычисляет моду для столбца column_name в таблице table_name:
SELECT column_name AS mode_value
FROM (
SELECT column_name, COUNT(*) AS frequency
FROM table_name
GROUP BY column_name
ORDER BY COUNT(*) DESC
LIMIT 1
) AS subquery
JOIN (
SELECT column_name, COUNT(*) AS frequency
FROM table_name
GROUP BY column_name
) AS subquery2 ON subquery.frequency = subquery2.frequency;
Если в данных есть несколько значений с одинаковой частотой, запрос покажет их все.
Медиана
Встроенной функции для вычисления медианы в SQL тоже нет. Один из распространенных способов, как это сделать, — использовать подзапросы и агрегатные функции. Вот один из способов:
SELECT AVG(column_name) AS median_value
FROM (
SELECT column_name
FROM table_name
ORDER BY column_name
LIMIT 2 — (SELECT COUNT(*) FROM table_name) % 2
OFFSET (SELECT (COUNT(*) — 1) / 2 FROM table_name)
) AS median_query;
Этот запрос вычисляет медиану для столбца column_name в таблице table_name. Он сначала упорядочивает значения столбца по возрастанию, затем выбирает одно или два средних значения в зависимости от того, четное ли количество значений. Если количество значений нечетное, выбирается одно среднее значение. Если количество значений четное, выбираются два средних значения и их среднее арифметическое — это и есть итоговая медиана.
Как вычислять значения в Python
В Python значения среднего арифметического и медианы полезны при анализе данных, статистических вычислениях, визуализации данных и во многих других задачах.
Для анализа данных используйте библиотеку pandas — в ней сможете работать с таблицами данных и вычислить среднее арифметическое и медиану для определенного столбца.
Если вам нужно проверить гипотезу или построить модель, попробуйте библиотеки NumPy и SciPy. У них есть функции для статистических вычислений, в том числе для вычисления среднего значения и медианы.
С библиотеками вроде Matplotlib или Seaborn можно легко создавать графики и визуализации со средними значениями.
Среднее арифметическое
Есть несколько способов, как вычислить среднее арифметическое на Python.
- Использовать встроенные функции Python:
# Создаем список значений
data = [10, 20, 30, 40, 50]
# Вычисляем среднее арифметическое
mean = sum(data) / len(data)
print(«Среднее арифметическое:», mean) - Использовать библиотеку NumPy — в ней есть более эффективные и удобные методы для работы с массивами чисел:
import numpy as np
# Создаем массив значений
data = np.array([10, 20, 30, 40, 50])
# Вычисляем среднее арифметическое
mean = np.mean(data)
print(«Среднее арифметическое:», mean)
Выбор метода зависит от ваших потребностей. Если вам не нужны сторонние библиотеки, хватит стандартных возможностей Python. Если нужны более продвинутые возможности или работаете с массивами данных, NumPy подойдет лучше.
Мода
Как вычислить моду на Python:
- Использовать библиотеку statistics (для версии Python 3.4 и выше):
import statistics
# Создаем список значений
data = [1, 2, 3, 4, 4, 5, 6, 6, 6]
# Вычисляем моду
mode = statistics.mode(data)
print(«Мода:», mode) - Использовать библиотеку SciPy:
from scipy import stats
# Создаем список значений
data = [1, 2, 3, 4, 4, 5, 6, 6, 6]
# Вычисляем моду
mode = stats.mode(data)
print(«Мода:», mode.mode[0]) # mode.mode — массив значений, поскольку мода может быть не одна - Использовать стандартные методы Python:
# Создаем список значений
data = [1, 2, 3, 4, 4, 5, 6, 6, 6]
# Вычисляем моду
mode = max(set(data), key = data.count)
print(«Мода:», mode)
Медиана
Вычислить медиану на Python тоже можно несколькими способами.
- Использовать библиотеку statistics (для версии Python 3.4 и выше):
import statistics
# Создаем список значений
data = [1, 3, 5, 7, 9]
# Вычисляем медиану
median = statistics.median(data)
print(«Медиана:», median) - Использовать библиотеку NumPy:
import numpy as np
# Создаем массив значений
data = np.array([1, 3, 5, 7, 9])
# Вычисляем медиану
median = np.median(data)
print(«Медиана:», median) - Использовать встроенные возможности Python:
# Создаем список значений
data = [1, 3, 5, 7, 9]
# Сортируем список
sorted_data = sorted(data)
# Вычисляем медиану
n = len(sorted_data)
if n % 2 == 0:
median = (sorted_data[n // 2 — 1] + sorted_data[n // 2]) / 2
else:
median = sorted_data[n // 2]
print(«Медиана:», median)
Освоить Python полезно для многих сфер. Но самая основная — это профессия Python-разработчика. Эти специалисты создают сайты, приложения, игры, которыми пользуемся мы все. И за свою работу получают хорошую зарплату.
Как совместно использовать среднее арифметическое и медиану
Это полезно, если нужно глубже понять данные и проанализировать, как они распределяются.
Центральная тенденция
Используйте среднее арифметическое и медиану вместе, чтобы оценить, насколько типичные значения сосредоточены вокруг центра.
Если среднее арифметическое и медиана близки друг к другу — значит, данные распределены симметрично. Если медиана сильно отличается от среднего арифметического — данные асимметричны или в ряду есть экстремальные значения.
Выбросы
Если среднее арифметическое значительно отличается от медианы, в данных есть выбросы. Анализ выбросов поможет понять, почему они появляются и как влияют на общее распределение данных.
Тип распределения
Используйте среднее арифметическое и медиану вместе с графиками распределения данных (например, гистограммами), чтобы лучше понять тип распределения. В сочетании с визуализацией данных среднее арифметическое и медиана помогут выявить особенности распределения: симметрию, асимметрию, мультимодальность и т. д.
Главное о среднем арифметическом
🟣 Среднее арифметическое — это математический способ найти «среднее» значение группы чисел. Вы складываете числа, которые есть в ряду, и делите получившуюся сумму на общее количество слагаемых.
🟣 Среднее значение помогает понять общие тенденции в данных.
🟣 Кроме среднего значения еще используют моду и медиану.
🟣 Мода — это самое частое значение в ряду.
🟣 Медиана — это буквально среднее значение. Медиана значит, что половина чисел больше нее и половина — меньше.
🟣 Моду и медиану считают более точными значениями. Они показывают реальную картину и не зависят от экстремальных выбросов в большую или меньшую сторону.
 Перейти в телеграм, чтобы получить результаты теста
Перейти в телеграм, чтобы получить результаты теста

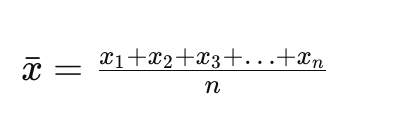








Добавить комментарий